- System of Units:-
(a) C.G.S (Centimeter-Grand-Second) system.
(b) F.P.S. (Foot-Pound-Second) system.
(c) M.K.S. (Meter-Kilogram--Second) system.
(d) M.K.S.A. (Meter-Kilogram-Second-Ampere) unit.
- Dimensional Formula:-
Dimensional formula of a physical quantity is the formula which tells us how and which of the fundamental units have been used for the measurement of that quantity.
- How to write dimensions of physical quantities:-
(a) Write the formula for that quantity, with the quantity on L.H.S. of the equation.
(b) Convert all the quantities on R.H.S. into the fundamental quantities mass, length and time.
(c) Substitute M, L and T for mass, length and time respectively.
(d) Collect terms of M,L and T and find their resultant powers (a,b,c) which give the dimensions of the quantity in mass, length and time respectively.
- Characteristics of Dimensions:-
(a) Dimensions of a physical quantity are independent of the system of units.
(b) Quantities having similar dimensions can be added to or subtracted from each other.
(c) Dimensions of a physical quantity can be obtained from its units and vice-versa.
(d) Two different physical quantities may have same dimensions.
(e) Multiplication/division of dimensions of two physical quantities (may be same or different) results in production of dimensions of a third quantity.
PHYSICAL QUANTITY
|
SYMBOL
|
DIMENSION
|
MEASUREMENT
| ||||
Length
|
s
|
L
|
Meter
|
m
| |||
Mass
|
M
|
M
|
Kilogram
|
Kg
| |||
Time
|
t
|
T
|
Second
|
Sec
| |||
Electric charge
|
q
|
Q
|
Coulomb
|
C
| |||
luminous intensity
|
I
|
C
|
Candela
|
Cd
| |||
Temperature
|
T
|
K
|
Kelvin
|
oK
| |||
Angle
|
q
|
none
|
Radian
|
None
| |||
Mechanical Physical Quantities (derived)
| |||||||
PHYSICAL QUANTITY
|
SYMBOL
|
DIMENSION
|
MEASUREMENT UNIT
| ||||
Area
|
A
|
L2
|
square meter
|
m2
| |||
Volume
|
V
|
L3
|
cubic meter
|
m3
| |||
velocity
|
v
|
L/T
|
meter per second
|
m/sec
| |||
angular velocity
|
w
|
T-1
|
radians per second
|
1/sec
| |||
acceleration
|
a
|
LT-2
|
meter per square second
|
m/sec2
| |||
angular acceleration
|
a
|
T-2
|
radians per square
second
|
1/sec2
| |||
Force
|
F
|
MLT-2
|
Newton
|
Kg m/sec2
| |||
Energy
|
E
|
ML2T-2
|
Joule
|
Kg m2/sec2
| |||
Work
|
W
|
ML2T-2
|
Joule
|
Kg m2/sec2
| |||
Heat
|
Q
|
ML2T-2
|
Joule
|
Kg m2/sec2
| |||
Torque
|
t
|
ML2T-2
|
Newton meter
|
Kg m2/sec2
| |||
Power
|
P
|
ML2T-3
|
watt or joule/sec
|
Kg m2/sec3
| |||
Density
|
D or ρ
|
ML-3
|
kilogram per
cubic meter
|
Kg/m3
| |||
pressure
|
P
|
ML-1T-2
|
Newton per square meter
|
Kg m-1/sec2
| |||
impulse
|
J
|
MLT-1
|
Newton second
|
Kg m/sec
| |||
Inertia
|
I
|
ML2
|
Kilogram square meter
|
Kg m2
| |||
luminous
flux
|
f
|
C
|
lumen (4Pi candle for point source)
|
cd sr
| |||
illumination
|
E
|
CL-2
|
lumen per
square meter
|
cd sr/m2
| |||
entropy
|
S
|
ML2T-2K-1
|
joule per degree
|
Kg m2/sec2K
| |||
Volume
rate of flow
|
Q
|
L3T-1
|
cubic meter
per second
|
m3/sec
| |||
kinematic
viscosity
|
n
|
L2T-1
|
square meter
|
m2/sec
| |||
per second
| |||||||
dynamic
viscosity
|
m
|
ML-1T-1
|
Newton second
per square meter
|
Kg/m sec
| |||
specific
weight
|
g
|
ML-2T-2
|
Newton
per cubic meter
|
Kg m-2/sec2
| |||
Electric
current
|
I
|
QT-1
|
Ampere
|
C/sec
| |||
emf, voltage,
potential
|
E
|
ML2T-2Q-1
|
Volt
|
Kg m2/sec2C
| |||
resistance or
impedance
|
R
|
ML2T-1Q-2
|
ohm
|
Kgm2 /secC2
| |||
Electric
conductivity
|
s
|
M-2L-2TQ2
|
mho
|
secC2/Kg m3
| |||
capacitance
|
C
|
M-1L-2T2 Q2
|
Farad
|
sec2C2/Kgm2
| |||
inductance
|
L
|
ML2Q-2
|
Henry
|
Kg m2 /C2
| |||
Current density
|
J
|
QT-1L-2
|
ampere per
square meter
|
C/sec m2
| |||
Charge density
|
r
|
QL-3
|
coulomb per cubic meter
|
C/m3
| |||
magnetic flux,
Magnetic induction
|
B
|
MT-1Q-1
|
weber per
square meter
|
Kg/sec C
| |||
magnetic
intensity
|
H
|
QL-1T-1
|
ampere per meter
|
C/m sec
| |||
magnetic vector
potential
|
A
|
MLT-1Q-1
|
weber/meter
|
Kg m/sec C
| |||
Electric
field intensity
|
E
|
MLT-2Q-1
|
volt/meter or
newton/coulomb
|
Kg m/sec2 C
| |||
Electric displacement
|
D
|
QL-2
|
coulomb per square meter
|
C/m2
| |||
permeability
|
m
|
MLQ-2
|
henry per meter
|
Kg m/C2
| |||
permittivity,
|
e
|
T2Q2M-1L-3
|
farad per meter
|
sec2C2/Kgm3
| |||
dielectric constant
|
K
|
M0L0T0
|
None
|
None
| |||
frequency
|
f or n
|
T-1
|
Hertz
|
sec-1
| |||
angular frequency
|
W
|
T-1
|
radians per second
|
sec-1
| |||
Wave length
|
l
|
L
|
Meters
|
M
| |||
- Principle of homogeneity:-
It states that “ the dimensional formulae of every term on the two sides of a correct relation must be same.”
- Types of error:-
(a) Constant errors:- An error is said to be constant error if it affects, every time, a measurement in a similar manner.
(b) Systematic errors:- Errors which come into existence by virtue of a definite rule, are called systematic errors.
(c) Random error or accidental error:- Error which takes place in a random manner and cannot be associated with a systematic cause are called random or accidental errors.
(d) Absolute error:- 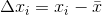
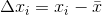
- Relative Error:-

- Percentage Error:-
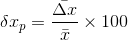


No comments:
Post a Comment