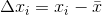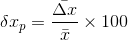Laws of Exponents || BASIC #MATHS FOR #ENTRANCE #EXAMS || by #cmrohityadav #edata
Laws of Exponents
The laws of exponents are demonstrated based on the powers they carry.
- Bases – multiplying the like ones – add the exponents and keep base same. (Multiplication Law)
- Bases – raise it with power to another – multiply the exponents and keep base same.
- Bases – dividing the like ones – ‘Numerator Exponent – Denominator Exponent’ and keep base same. (Division Law)
Let ‘a’ is any number or integer (positive or negative) and ‘m’, ‘n’ are positive integers, denoting the power to the bases, then;
Multiplication Law
As per the multiplication law of exponents, the product of two exponents with the same base and different powers equals to base raised to sum of the two powers or integers.
Division Law
When two exponents having same bases and different powers are divided, then it results in base raised to difference of the two powers.
Negative Exponent Law
Any base if has a negative power, then it results in reciprocal but with positive power or integer to the base.
Exponents and Powers Rules
The rules of exponents are followed by the laws. Let us have a look on them with a brief explanation.
Suppose ‘a’ & ‘b’ are the integers and ‘m’ & ‘n’ are the values for powers, then the rules for exponents and powers are given by:
i) a0 = 1
As per this rule, if the power of any integer is zero, then the resulted output will be unity or one.
Example: 50 = 1
ii) (am)n = a(mn)
‘a’ raised to the power ‘m’ raised to the power ‘n’ is equal to ‘a’ raised to the power product of ‘m’ and ‘n’.
Example: (52)3 = 52 x 3
iii) am × bm =(ab)m
The product of ‘a’ raised to the power of ‘m’ and ‘b’ raised to the power ‘m’ is equal to the product of ‘a’ and ‘b’ whole raised to the power ‘m’.
Example: 52 × 62 =(5 x 6)2
iv) am/bm = (a/b)m
The division of ‘a’ raised to the power ‘m’ and ‘b’ raised to the power ‘m’ is equal to the division of ‘a’ by ‘b’ whole raised to the power ‘m’.
Exponents and Power Solved Questions
Example 1: Write 7 x 7 x 7 x 7 x 7 x 7 x 7 x 7 in exponent form.
Solution:
In this problem 7s are written 8 times, so the problem can be rewritten as an exponent of 8.
7 x 7 x 7 x 7 x 7 x 7 x 7 x 7 = 78.
Example 2: Write below problems like exponents:
- 3 x 3 x 3 x 3 x 3 x 3
- 7 x 7 x 7 x 7 x 7
- 10 x 10 x 10 x 10 x 10 x 10 x 10
Solution:
- 3 x 3 x 3 x 3 x 3 x 3 = 36
- 7 x 7 x 7 x 7 x 7 = 75
- 10 x 10 x 10 x 10 x 10 x 10 x 10 = 107
Example 3: Simplify 253/53
Solution:
Using Law: am/bm = (a/b)m
253/53 can be written as (25/5)3 = 53 = 125.
Exponents and Powers Applications
Scientific notation uses the power of ten expressed as exponents, so we need a little background before we can jump in. In this concept, we round out your knowledge of exponents, which we studied in previous classes.
The distance between the Sun and the Earth is 149,600,000 kilometers. The mass of the Sun is 1,989,000,000,000,000,000,000,000,000,000 kilograms. The age of the Earth is 4,550,000,000 years. These numbers are way too large or small to memorize in this way. With the help of exponents and powers these huge numbers can be reduced to a very compact form and can be easily expressed in powers of 10.
Now, coming back to the examples we mentioned above, we can express the distance between the Sun and the Earth with the help of exponents and powers as following:
Distance between the Sun and the Earth 149,600,000 = 1.496× 10 × 10 × 10 × 10 × 10× 10 × 10 = 1.496× 108 kilometers.
Mass of the Sun: 1,989,000,000,000,000,000,000,000,000,000 kilograms = 1.989 × 1030 kilograms.
Age of the Earth: 4,550,000,000 years = 4. 55× 109 years